Mathematics PhD



For my PhD I modelled tumour growth. To do this I first numerically solved a system of partial differential equations, and then performed a significant amount of Mathematics analysis on the system of equations as well as the numerical solutions. This was a Mathematics PhD, but involved approximately 50% programming. I was engaged in independent (supervised) research, including Mathematical analysis, scientific programming, and producing literature (a paper (arxiv link here) and a thesis (link to the publication here)). I was also involved in teaching undergraduate students, and marking work. The system of equations I numerically solved and analysed is shown below, along with a diagram detailing the notation for the interior and exterior of the tumour.
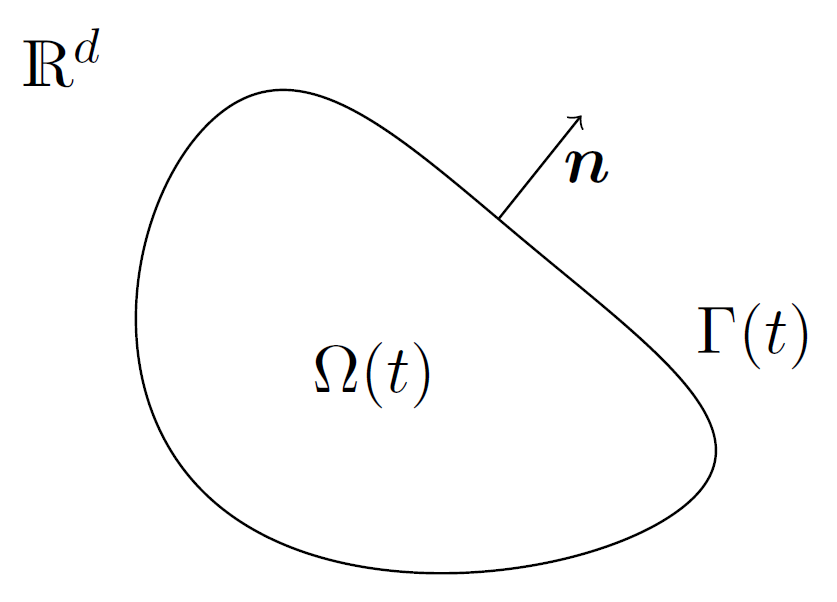
Since I wanted to use a sharp interface approach and finite element methods, I had to maintain an evolving mesh on this moving boundary. This is a highly complex problem, that has no standard solution. In order to generate a solution, I had to implement a number of algorithms from the literature. I settled on a combination of approaches. The first approach smooths the velocity of the boundary over the interior of the tumour, allowing the mesh to evolve with it. The second re-builds the mesh when it reaches a point at which it can no longer be smoothed. You can see this below.

